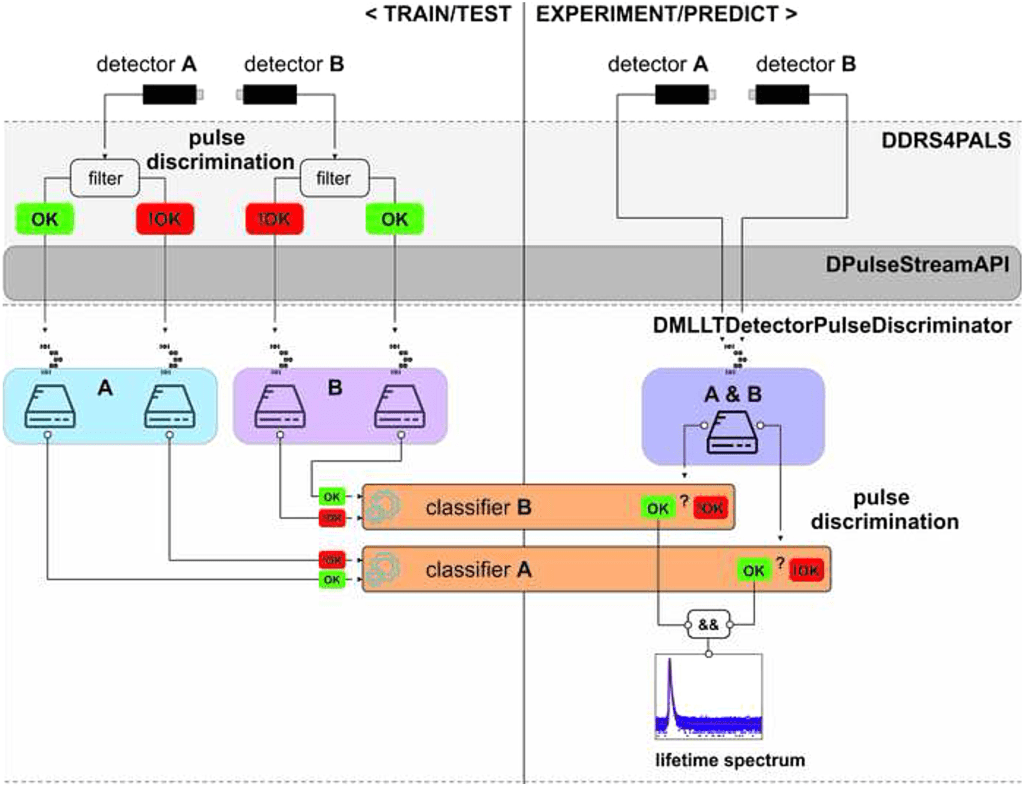
Task: Detector pulse discrimination in positron annihilation lifetime spectroscopy (PALS)
Description: A supervised machine learning (ML) model based on a naive Bayes classification model using a normally distributed likelihood as a novel approach for shape-sensitive detector pulse discrimination.
The model validation and testing in the associated reference publication focuses on lifetime spectra generated by applying the method of PALS. However, this ML approach can be easily applied (or adapted) for various spectroscopy techniques using pulses from single-photon detectors (e.g. photomultipliers, (avalanche) photo diodes) thanks to an implemented user-friendly python-based framework (DMLLT Detector Pulse Discriminator), which allows training and testing of any kind of detector pulses. Furthermore, a simple exchange protocol serves for the dataset transfer. In the particular case of lifetime spectroscopy applications, this framework further provides the generation of lifetime spectra from experimental data, i.e. pulse pairs acquired on real samples.
For the training and testing datasets of both PMTs A and B, two separate streams of about 10.000 detector pulses each, representing the respective correct and false labelled pulses,4 have been obtained on pure aluminium (5N) given an independent dataset. The discrimination of the detector pulses and, thus, their labelling was accomplished automatically by applying pulse shape and pulse area filtering provided by DDSR4PALS v1.09 software. Hence, detector pulses, which have been rejected by the filters are assigned as being false, whereas otherwise they are termed correct.
Once the classifiers are optimized, the resulting lifetime spectra can be easily generated from the experimental datasets without applying any filtering on the detector pulses as their discrimination is finally done by the classifier. Hence, a calculation of the time differences between the acquired pulse pairs (i.e. the individual lifetime) and, finally, its contribution to the resulting lifetime spectrum is only processed if both respective classifiers predict them as being correct.
Results: A remarkable low number of less than 20 labelled training pulses is sufficient to achieve comparable results as of applying physically filtering. Hence, the proposed model represents a potential alternative.
In the following, the evaluation of each learned classifier corresponding to a specific set of parameters on the grid was obtained from the same number of about 8000 pulses of the testing dataset for each class (correct and false pulses) of the respective detectors A and B. As indicated in the figure below, a significant improvement of about 9.3% in the prediction accuracy was achieved for the pulses of detector A by applying median filtering using a window size of 11. However, only slight improvements of about 1.5% in the prediction accuracy were achieved for detector B using a window size of 5, whereby its initial prediction accuracy, i.e. without median filtering, and its optimized prediction accuracy are considerably higher with respect to detector A of about 9.9% and 2.6%, respectively. Furthermore, it can be observed for both detectors A and B that the highest prediction accuracies are already obtained at a very low number of learned correct and false pulses (<20 pulses) by applying median filtering (window sizes: 5 & 11). This is typical for naive Bayes classifiers and a significant advantage of using this approach.
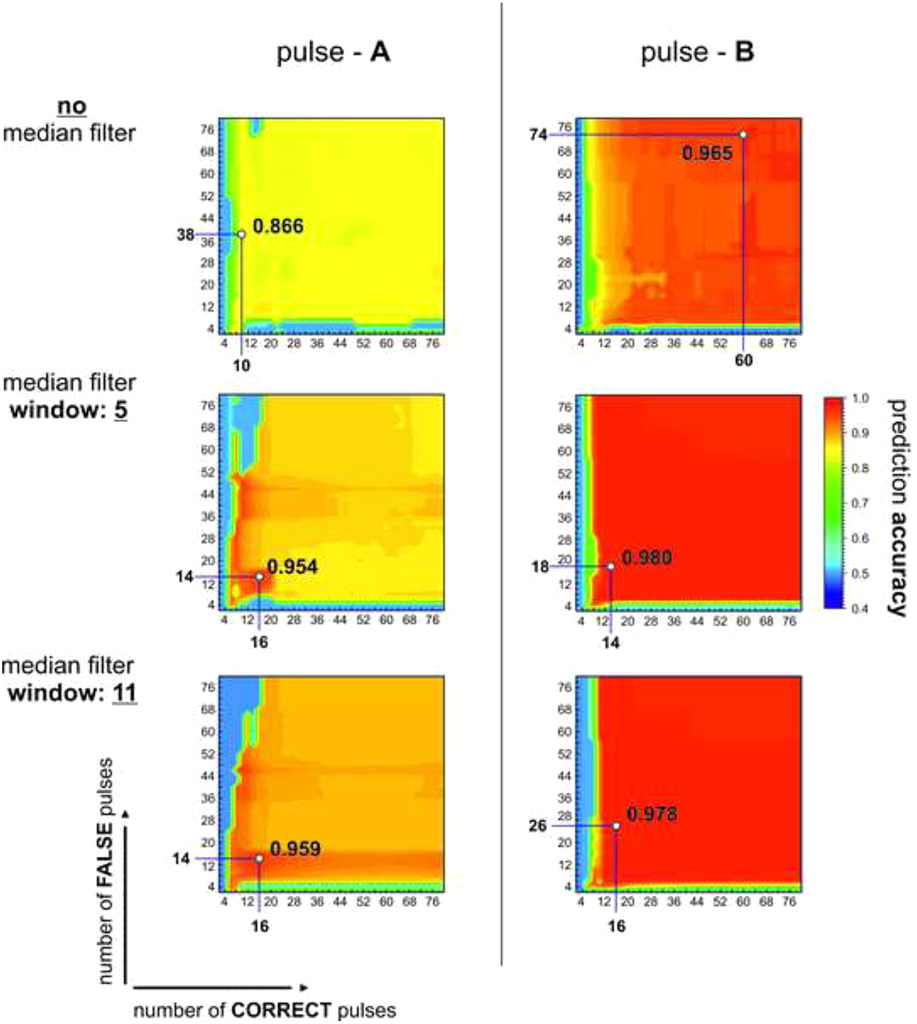
Claim: The model implements a streamlined approach and a very convenient way for the discrimination (filtering) of detector pulses and, thus, the generation of high-quality lifetime spectra as it only requires a remarkable low number (<20) of detector pulses for training the classifier. Nevertheless, comparable results are achieved in terms of spectra quality and peak-to-background ratio as of applying physically filtering (e.g. pulse shape or pulse area filters). Thus, the filtering procedures may be considered as obsolete as they can be replaced at nearly no costs by the learned classifier obtained from a small dataset of pulses. Moreover, its selection can be even manually applied by the user, meaning that this required small number of correct and false pulses can be easily picked by hand. This might be managed by implementing a kind of pulse selection tool in the underlying acquisition software allowing the user to distinguish a displayed pulse as being correct (top) or false (flop).
